Question

Evaluate (if possible) the sine, cosine, and tangent of the real number t. (If not possible, enter IMPOSSIBLE.)

3π
2
t=-
sin(t)=
cos(t) =
tan(t)=

Answer 1

Answers:

sin(t) = 1

cos(t) = 0

tan(t) = impossible

========================

Explanation

Refer to the unit circle diagram shown below. This diagram shows up a lot in trigonometry. It's something you should memorize or have as a quick reference sheet.

On the unit circle, you'll find that angle -3pi/2 radians isn't shown. But we can fix this by adding a full revolution of 2pi radians.

-3pi/2 + 2pi = -3pi/2 + 4pi/2 = (-3pi+4pi)/2 = pi/2

In short,

-3pi/2 + 2pi = pi/2

The angle -3pi/2 is coterminal with pi/2. These two angles both point directly north.

----------

Now we can use the unit circle.

The diagram shows that (x,y) = (0,1) when the angle is pi/2 radians (aka 90 degrees).

• x = cos(theta) = 0
• y = sin(theta) = 1

This is how we end up with the first two answers of

sin(t) = 1 and cos(t) = 0

Divide sine over cosine to determine tangent.

tan(t) = sin(t)/cos(t)

tan(t) = 1/0

tan(t) = undefined

We cannot divide by zero.

Answer 2

`\sf sin(t) = \boxed{\sf 1}`

`\sf cos(t) = \boxed{\sf 0}`

`\sf tan(t) = \boxed{\sf impossible}`

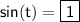
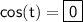
Explanation:

Given:

`\sf t = -(3\pi)/(2)`

Solution:

To evaluate the sine, cosine, and tangent of the real number t, we can use the properties of trigonometric functions at this angle.

1. Sine (sin):

The sine function is positive in the second and fourth quadrants.

In the second quadrant, it has the same absolute value as in the fourth quadrant, but it's negative.

So, for
`\sf t = -(3\pi)/(2)` (which is in the third quadrant), the sine function is:

`\sf sin\left(-(3\pi)/(2)\right) = - sin\left((\pi)/(2)\right) = -* -1= 1`

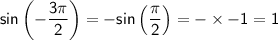
So,

`\sf sin\left(-(3\pi)/(2)\right) = 1`

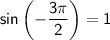
2. Cosine (cos):

The cosine function is negative in the second and third quadrants.

For
`\sf t = -(3\pi)/(2)`(which is in the third quadrant), the cosine function is:

`\sf cos\left(-(3\pi)/(2)\right) = -\cos\left((\pi)/(2)\right) = 0`

So,

`\sf cos\left(-(3\pi)/(2)\right) = 0`

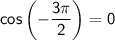
3. Tangent (tan):

The tangent function is positive in the second and fourth quadrants.

For
`\sf t = -(3\pi)/(2)` (which is in the third quadrant), the tangent function is undefined because
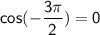`\sf cos(-(3\pi)/(2)) = 0` , and division by zero is undefined.

So,
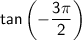`\sf tan\left(-(3\pi)/(2)\right)` is undefined or impossible.