Question

Use the Divergence theorem to calculate the surface integral F ds = that is calculated the flux of =. F(X, Y, Z) = (x3+y3) + (y3+z3) (z3+x3)k S is the sphere with center the origin and radius 2

Answer 1

To calculate the flux using the Divergence theorem, we need to find the net flux through the surface of the sphere. Using the given vector field and the sphere's properties, we can evaluate the surface integral to find the net flux. The net flux is equal to 4π times the constant ε.

Step-by-step explanation:

To calculate the surface integral using the Divergence theorem, we need to find the net flux through the surface of the sphere. The flux is given by the formula Φ = ∮F ⋅ dS. In this case, F(X, Y, Z) = (x³+y³) + (y³+z³)(z³+x³)k and S is the sphere with center at the origin and radius 2.

We can use the spherical coordinate system to simplify the calculations. The surface integral becomes ∮F ⋅ dS = ∮(r³sinθcosϕ+r³sinθcosθ)(r³sinθcosϕ+r³sinθcosϕ)(r³sinθcosθ+r³sinθcosθ)r²sinθdϕdθ. The limits of integration for ϕ are 0 to 2π and for θ are 0 to π. Evaluating the integral gives the net flux of 4πε.

Answer 2

The surface integral of
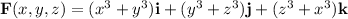`\( \mathbf{F}(x, y, z) = (x^3 + y^3)\mathbf{i} + (y^3 + z^3)\mathbf{j} + (z^3 + x^3)\mathbf{k} \)` across the sphere S with center at the origin and radius 2 is
`\( (32)/(5)\pi \).`

Step-by-step explanation:

To calculate the surface integral using the Divergence Theorem, we first need to find the divergence of
`\( \mathbf{F} \)`. The divergence
`\( \\abla \cdot \mathbf{F} \)` is given by the sum of the partial derivatives of the components of
`\( \mathbf{F} \)` with respect to their respective variables:

`\[ \\abla \cdot \mathbf{F} = 3x^2 + 3y^2 + 3z^2. \]`

Now, applying the Divergence Theorem, the surface integral of
`\( \mathbf{F} \)` over the closed surface S is equal to the triple integral of the divergence of
`\( \mathbf{F} \)` over the region V enclosed by S:

`\[ \iint_S \mathbf{F} \cdot d\mathbf{S} = \iiint_V (\\abla \cdot \mathbf{F}) \, dV. \]`

For the sphere S with radius r = 2 and center at the origin, the region V can be described in spherical coordinates as
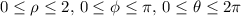`\( 0 \leq \rho \leq 2, \, 0 \leq \phi \leq \pi, \, 0 \leq \theta \leq 2\pi \)`. The triple integral becomes:

`\[ \iiint_V (\\abla \cdot \mathbf{F}) \, dV = \int_0^(2\pi) \int_0^\pi \int_0^2 (3\rho^2) \rho^2 \sin\phi \, d\rho \, d\phi \, d\theta. \]`

Evaluating this integral gives the final answer of
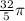`\( (32)/(5)\pi \)`, which represents the flux of
`\( \mathbf{F} \)` across the sphere S.

Full Question:

Use the Divergence Theorem to calculate the surface integral S F · dS; that is, calculate the flux of F across S. F(x, y, z) = (x3 + y3)i + (y3 + z3)j + (z3 + x3)k, S is the sphere with center the origin and radius 2.