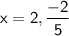Question

Find one value of x that is a solution to the equation: (5x+2)² +15x+6=0

Answer 1

`2 , (-2)/(5)`

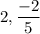
Explanation:

Finding the solution for a polynomial:

Expand (5x +2)² using the algebraic identity (a+ b)² = a² + 2ab + b²

Hert a = 5x and b = 2

(5x + 2)² + 15x + 6 =0

(5x)² + 2*5x*2 + 2² + 15x + 6 =0

25x² + 20x + 4 + 15x + 6 = 0

25x² + 20x + 15x + 6 + 4 =0

Combine the like terms,

25x² + 35x + 10 =0

Divide the entire equation by 5,

5x² + 7x + 2 = 0

Sum = 7

Product = 10

Factors = 5 , 2

Rewrite the middle term using the factors,

5x² + 5x + 2x + 2 = 0

5x(x + 1) + 2(x + 1) = 0

(x + 1)(5x + 2) = 0

x + 1 = 0 ; 5x + 2 = 0

x = -1 ; 5x = -2

`\sf x = (-2)/(5)`

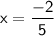
Answer:

`\sf x = 2 , (-2)/(5)`