Question

Let (2 -7) be a point on the terminal side of theta. Find the exact values of cos0, csc0, tan0.

Answer 1

Answers:

`\cos(\theta) = (2)/(√(53)) = (2√(53))/(53)\\\\\tan(\theta) = -(7)/(2)\\\\\csc(\theta) = -(√(53))/(7)\\\\`

=======================================================

Step-by-step explanation

The terminal point is located at (x,y) = (2,-7)

Let's calculate the distance from the origin to the terminal point.

`r = √(x^2+y^2)\\\\r = √(2^2+(-7)^2)\\\\r = √(4+49)\\\\r = √(53)\\\\`

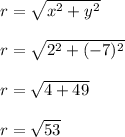
From there we would write the following:

`\cos(\theta) = \frac{\text{x}}{\text{r}} = (2)/(√(53)) = (2√(53))/(53)\\\\\tan(\theta) = \frac{\text{y}}{\text{x}} = -(7)/(2)\\\\\csc(\theta) = \frac{\text{r}}{\text{y}} = -(√(53))/(7)\\\\`

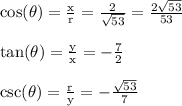
Side notes:

• The terminal point (2,-7) is in quadrant 4. This is the southwest quadrant.
• Cosine is positive in quadrant 4, while tangent and cosecant are negative in this quadrant.
• Rationalizing the denominator may be optional.
• x = adjacent
• y = opposite
• r = hypotenuse
• cosecant is the reciprocal of sine