Answer:
A) -6x+3y = 12
Explanation:
Let's take two points from the straight line.
(-2,0) and (0, 4).
Now
We can find the equation of the line by using the point-slope form of the equation of a line:
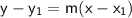
where:
- (x1, y1) are the coordinates of one of the points on the line (in this case, (-2, 0)),
- m is the slope of the line.
First, find the slope (m) using the two given points (-2, 0) and (0, 4):
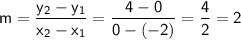
Now that we have the slope, we can use one of the points, such as (0,4), in the point-slope form:
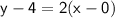
Simplify:
y -4 = 2x
Keep the x and y terms in left side and constant on right side,
-2x+y = 4
Since it's not in a options, so
Multiply both sides by 3.
-6x+3y = 12
Therefore, answer is:
A) -6x+3y = 12