Question

Express the function graphed on the axes below as a piecewise function​

Answer 1

`y=\begin{cases}2x+10,&-6\le x < -3\\-x+1,&-3 < x < 2\end{cases}`

Explanation:

You want a piecewise function that matches the given graph.

Left piece

The segment on the left begins at (-6, -2) and ends at (-3, 4). The right endpoint is not included in the domain for this segment: -6 ≤ x < -3.

The slope of the segment is given by the formula ...

m = (y2 -y1)/(x2 -x1)

m = (4 -(-2))/(-3 -(-6)) = 6/3 = 2

The y-intercept of the segment can be found from ...

b = y -mx

b = -2 -(2)(-6) = 10

So, the slope-intercept equation for the left segment is ...

y = 2x +10 . . . . for -6 ≤ x < -3

Right piece

Similarly, we can find the slope and y-intercept of the segment between (-3, 4) and (2, -1). The domain of this segment does not include the endpoints: -3 < x < 2.

m = (-1 -4)/(2 -(-3)) = -5/5 = -1

b = 4 -(-1)(-3) = 1

Then the slope-intercept equation for the right segment is ...

y = -x +1 . . . . for -3 < x < 2

The piecewise function is ...

`\boxed{y=\begin{cases}2x+10,&-6\le x < -3\\-x+1,&-3 < x < 2\end{cases}}`

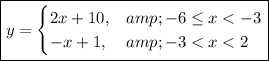
<95141404393>