Question

Assuming a compressor efficiency of 80 percent and a turbine efficiency of 85 percent, determine (a) the back work ratio, (b) the thermal efficiency

Answer 1

To determine the back work ratio and thermal efficiency, more information is required such as the work done by the compressor and turbine or the heat input to the thermodynamic cycle. Back work ratio is typically calculated as the ratio of compressor work to turbine work, while thermal efficiency is the net work output divided by the heat input.

Step-by-step explanation:

The question involves thermodynamics in an engineering context, specifically relating to the efficiencies of compressors and turbines within a thermodynamic cycle. The back work ratio is defined as the ratio of the compressor work to the turbine work, and thermal efficiency is the ratio of the net work output of the cycle to the heat input.

Given: Compressor efficiency = 80%, Turbine efficiency = 85%.

(a) To calculate the back work ratio (BWR), we need more data such as heat input or the work done by the compressor and the turbine. Normally, BWR can be determined using the formula BWR = Work_compressor / Work_turbine.

(b) For thermal efficiency (η), it's generally calculated using the formula η = (Work_output / Heat_input) × 100%. In this case, additional information such as the heat input to the cycle or the net work output is required to calculate the thermal efficiency. Without this additional data, it's not possible to calculate the exact values for back work ratio and thermal efficiency.

Answer 2

The back work ratio is defined as the ratio of the compressor work to the turbine work. For an ideal Brayton cycle (where the compressor and turbine processes are isentropic), this is calculated as follows:

`\[ BWR = (W_c)/(W_t) \]`

Thermal efficiency for a Brayton cycle is defined as the net work done by the system divided by the heat input:

`\[ \eta_(th) = (W_(net))/(Q_(in)) \]`

To determine the back work ratio and thermal efficiency for a system with a compressor efficiency of 80% and a turbine efficiency of 85%, we need to follow a step-by-step thermodynamic analysis. This kind of analysis is typically used in the context of a simple Brayton cycle, which is a common model for gas turbine engines.

Step 1: Understand the Brayton Cycle

The Brayton cycle consists of four processes:

1. Isentropic compression (in a compressor).

2. Constant pressure heat addition (in a combustion chamber).

3. Isentropic expansion (in a turbine).

4. Constant pressure heat rejection (in the exhaust).

Step 2: Assumptions

- The cycle operates in a steady flow.

- Changes in kinetic and potential energy are negligible.

- The working fluid behaves as an ideal gas.

Step 3: Define Given Efficiencies

- Compressor efficiency
`(\(\eta_c\)) = 80% or 0.8.`

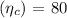
- Turbine efficiency
`(\(\eta_t\)) = 85% or 0.85.`

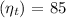
Step 4: Back Work Ratio (BWR)

The back work ratio is defined as the ratio of the compressor work to the turbine work. For an ideal Brayton cycle (where the compressor and turbine processes are isentropic), this is calculated as follows:

`\[ BWR = (W_c)/(W_t) \]`

However, with non-ideal conditions (real efficiencies), the work input and output are different. The actual work of the compressor
`(\(W_c\)) and turbine (\(W_t\))`can be adjusted for efficiency:

`\[ W_c(actual) = (W_c(ideal))/(\eta_c) \]`

`\[ W_t(actual) = W_t(ideal) * \eta_t \]`

The ideal work can be expressed in terms of specific heats and temperature differences (for an ideal gas), but without specific temperatures or pressure ratios, we can't calculate this exactly. Instead, we can express BWR in terms of efficiencies:

`\[ BWR = (W_c(actual))/(W_t(actual)) = (W_c(ideal) / \eta_c)/(W_t(ideal) * \eta_t) \]`

Since we don't have the exact values for
`\(W_c(ideal)\) and \(W_t(ideal)\),`we cannot calculate a numeric value for BWR without additional data.

Step 5: Thermal Efficiency
`(\(\eta_(th)\))`

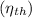
Thermal efficiency for a Brayton cycle is defined as the net work done by the system divided by the heat input:

`\[ \eta_(th) = (W_(net))/(Q_(in)) \]`

Where
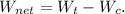`\(W_(net) = W_t - W_c\).` Again, without specific values for work and heat transfer, we can't compute a numeric value. However, we can express it in terms of given efficiencies:

`\[ \eta_(th) = (W_t(actual) - W_c(actual))/(Q_(in)) \]`