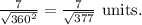Final Answer:
The distance between the lines
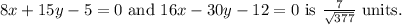
Step-by-step explanation:
To find the distance between two skew lines, we'll use the formula for the distance between a point and a line. We need to select a point on one line and then find the perpendicular distance from that point to the other line. The normal vectors to the lines will help us achieve this.
Given the equations of the lines are
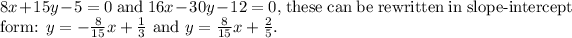
The direction vectors of these lines are
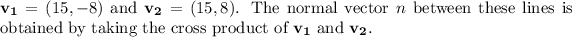
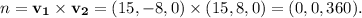
The magnitude of the normal vector
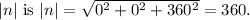 To find the distance \(d\) between the lines, divide the absolute value of the constant term in one of the line equations by the magnitude of the normal vector:
To find the distance \(d\) between the lines, divide the absolute value of the constant term in one of the line equations by the magnitude of the normal vector:
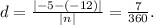
Therefore, the distance between the lines is