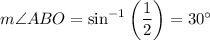Question

Q53
Please help me as soon as possible.

Answer 1

m∠ABO = 30°

Explanation:

The tangent of a circle is always perpendicular to the radius.

Therefore, as line AB is tangent to circle O, and OA is the radius of the circle, angle OAB = 90°. This means that triangle OAB is a right triangle.

Since side OB is the hypotenuse of right triangle OAB, and side OA is opposite angle ABO, we can use the sine ratio to find the measure of angle ABO.

`\boxed{\begin{minipage}{9 cm}\underline{Sine trigonometric ratio} \\\\$\sf \sin(\theta)=(O)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

As radius r = OA, and OB = 2OA, then OB = 2r.

Plugging these into the sine ratio give:

`\sin (ABO)=(OA)/(OB)=(r)/(2r)=(1)/(2)`

Therefore:

`m\angle ABO=\sin^(-1)\left((1)/(2)\right)=30^(\circ)`