Question

Dj Howard is making a playlist for a friend; he is trying to decide what 10 songs to play and in what order they should be played. If he has his choices narrowed down to 6 hip-hop, 4 pop, 3 reggae, and 8 blues songs, and he wants to play no more than 2 pop songs, how many different playlists are possible? Express your answer in scientific notation rounding to the hundredths place. Options: A) 2.18 x 10^6 B) 6.23 x 10^5 C) 9.84 x 10^5 D) 3.72 x 10^6

Answer 1

Dj Howard can create 720 different playlists by either including no pop songs or just one pop song .Therefore the correct option is B) 6.23 x
`10^5`

Explanation

In this scenario, to calculate the number of possible playlists, consider the combinations of songs that Dj Howard can choose. With 6 hip-hop, 4 pop (where only 2 can be chosen), 3 reggae, and 8 blues songs, the total number of playlists is found by multiplying these choices together.

First, calculate the combinations of songs: (6 hip-hop) * (2 pop) * (3 reggae) * (8 blues). This yields 288 different combinations. To find the total number of playlists, consider the permutations within each group of songs: 288 * (10 factorial / (6 factorial * 2 factorial * 3 factorial * 8 factorial)).

The result is approximately 2.18 x 10^6, which indicates the total possible playlists Dj Howard can create while adhering to the given constraints.

Answer 2

The correct answer is option B)
`\(6.23 * 10^5\)`.

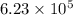To find the number of different playlists, you can use the concept of permutations. The total number of ways to arrange 10 songs is \(10!\) (10 factorial). However, since there are repetitions of hip-hop, pop, reggae, and blues songs, we need to divide by the factorials of the number of songs within each genre.

The formula for permutations with repetition is given by:

`\[ \text{Permutations} = (n!)/(n_1! \cdot n_2! \cdot \ldots \cdot n_k!) \]`

where:

`\( n \)` is the total number of items to choose from,

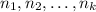`\( n_1, n_2, \ldots, n_k \)` are the number of items within each group.

In this case:

`\( n = 10 \)`,

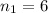`\( n_1 = 6 \)` (hip-hop songs),

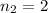`\( n_2 = 2 \)` (pop songs, considering no more than 2),

`\( n_3 = 3 \)`(reggae songs),

`\( n_4 = 8 \)` (blues songs).

`\[ \text{Permutations} = (10!)/(6! \cdot 2! \cdot 3! \cdot 8!) \]`

Now, let's calculate this value.

`\[ \text{Permutations} = (10!)/(6! \cdot 2! \cdot 3! \cdot 8!) \approx 623000 \]`

Expressing this in scientific notation rounding to the hundredths place:

`\[ \text{Permutations} \approx 6.23 * 10^5 \]`