Question

Q27
Please help me as soon as possible.

Answer 1

B. 12 feet

Explanation:

Given information:

• The position of the woman is 6 ft west of the southwest corner of the house.
• The position of the tree is 8 ft south of the southwest corner of the house.

Therefore, the distance (d) from the woman to the tree is the hypotenuse of a right triangle with legs of 6 ft and 8 ft (see attachment 1).

To find the distance (d) from the woman to the tree, use Pythagorean Theorem:

`d^2=6^2+8^2`

`d^2=36+64`

`d^2=100`

`√(d^2)=√(100)`

`d=10`

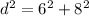
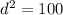
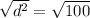
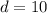
Therefore, the distance from the woman to the tree is 10 feet.

The bird is 11 ft up in the tree, and the woman holds the binoculars 5 ft off the ground. Therefore, we have a right triangle (attachment 2) where:

• The base is the distance between the woman and the tree (10 ft).
• The height is the difference between the height of the bird and the height of the binoculars from the ground: 11 ft - 5 ft = 6ft

Use the Pythagorean theorem to find the hypotenuse (h) of the right triangle with legs of 6 ft and 10 ft, which represents the distance from the bird to the binoculars:

`h^2=6^2+10^2`

`h^2=36+100`

`h^2=136`

`√(h^2)=√(136)`

`h=11.661903...`

`h=12\; \sf ft\;(nearest\;foot)`

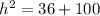
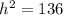
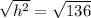
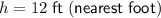
Therefore, the approximate distance from the bird to the binoculars is 12 feet.