Question

Q23
Please help me as soon as possible.

Answer 1

`\textsf{A.} \quad √(7)`

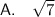
Explanation:

A rational number is a real number that can be expressed as the quotient or fraction of two integers, where the denominator is non-zero.

To determine which of the given answer options is not a rational number, we can evaluate each answer.

`\hrulefill`

7 is a prime number, meaning its only factors are 1 and itself.

Since 7 cannot be expressed as the square of an integer, we cannot take its square root to obtain a rational number.

Therefore, √7 cannot be represented as a fraction and is considered an irrational number.

`\hrulefill`

7.29 can be written 729/100. Therefore:

`√(7.29)=\sqrt{(729)/(100)}=(√(729))/(√(100))`

The square root of 729 is 27, and the square root of 100 is 10. Therefore:

`√(7.29)=\sqrt{(729)/(100)}=(√(729))/(√(100))=(27)/(10)`

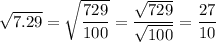
So, as
`√(7.29)` can be expressed as the fraction 27/10, it is a rational number.

`\hrulefill`

As 196 is equal to 14 × 14, we can rewrite 196 as 14². Therefore:

`√(196)=√(14^2)`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`√(196)=√(14^2)=14`

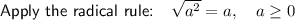
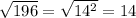
As any integer can be written as a fraction by dividing it by 1, the integer 14 can be written as 14/1:

`√(196)=√(14^2)=14=(14)/(1)`

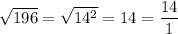
Therefore, as
`√(196)` can be expressed as the fraction 14/1, it is a rational number.

`\hrulefill`

Rewrite 4 and 9 as 2² and 3². Therefore:

`\sqrt{(4)/(9)}=\sqrt{(2^2)/(3^2)}=(√(2^2))/(√(3^2))`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`\sqrt{(4)/(9)}=\sqrt{(2^2)/(3^2)}=(√(2^2))/(√(3^2))=(2)/(3)`

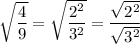
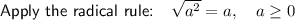
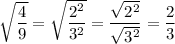
So, as √(4/9) can be expressed as the fraction 2/3, it is a rational number.

`\hrulefill`

To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, add this to the numerator of the fraction, and place the answer over the denominator:

`4(1)/(5)=(4 \cdot 5+1)/(5)=(20+1)/(5)=(21)/(5)`

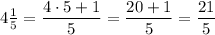
Therefore, as 4¹/₅ can be expressed as the fraction 21/5, it is a rational number.