Question

Starting at time t = 0, an object moves along a straight line. Its coordinate in meters is given by x(t) = 75t - 1.0t3 , where t is in s. When velocity (v) of the object = 0, the value of its acceleration is : (Ans: -30 m/s2 )

Answer 1

Step-by-step explanation:

Take the derivative of position to get velocity.

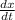`(dx)/(dt\\)` = v(t) = 75 -
`3t^(2)`

Find when the velocity equals 0.

0 = 75 -
`3t^(2)`

-75 = -
`3t^(2)`

25 =
`t^(2)`

t = ± 5 seconds

Now find the acceleration at t = 5 seconds. Because time cannot be negative, disregard the -5 second answer.

Take the derivative of velocity to get acceleration

a =
`(dv)/(dt) = -6t`

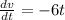
Now plug in 5

a = -6*5

a = -30
`m/s^(2)`