Question

The cross-sectional of a rivet is 3.46 cm2 Calculate the diameter of the hole?​

Answer 1

The diameter of the hole for the rivet is approximately 2.11 cm.

Step-by-step explanation:

The cross-sectional area of a circle is calculated using the formula \
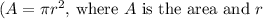`(A = \pi r^2\), where \(A\) is the area and \(r\)`is the radius of the circle. In this case, the cross-sectional area of the hole is given as 3.46 cm².

The formula for the area of a circle is \(A = \pi r^2\), where the area given is 3.46 cm². To find the radius, rearrange the formula to solve for \(r\):

`\[A = \pi r^2\]\[r^2 = (A)/(\pi)\]\[r = \sqrt{(A)/(\pi)}\]\[r = \sqrt{\frac{3.46 \, \text{cm}^2}{\pi}}\]\[r \approx 1.05 \, \text{cm}\]`

The diameter of the hole is twice the radius. Therefore, the diameter of the hole for the rivet is approximately
`\(2 * 1.05 \approx 2.11 \, \text{cm}\).`

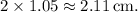
Understanding how to calculate geometric dimensions like diameter or radius from given area or vice versa is crucial in engineering and construction applications, particularly when dealing with components like rivets, bolts, or fasteners.

Answer 2

To calculate the diameter of the hole, we need to determine the radius of the cross-sectional area by using the formula A = πr², where A is the area and r is the radius. Rearrange the formula to find r and substitute the given cross-sectional area to find the radius. Finally, double the radius to get the diameter of the hole.

Step-by-step explanation:

To calculate the diameter of the hole, we need to determine the radius of the cross-sectional area. The formula for the cross-sectional area is A = πr², where A is the area and r is the radius. Rearranging the formula, we have r . Substituting the given cross-sectional area of 3.46 cm², we find r = 1.05 cm. Therefore, the diameter of the hole is twice the radius, which is 2.10 cm.