Question

An object moves in a circle at constant speed. The work done by centripetal force is zero because a. The displacement for each revolution is zero b. The average force for each revolution is zero c. The centripetal force is perpendicular to the velocity d. The magnitude of the acceleration is zero"

Answer 1

The work done by centripetal force is zero because the centripetal force is perpendicular to the velocity of an object in circular motion.

Step-by-step explanation:

The question is related to the concept of work done by centripetal force on an object moving in uniform circular motion. Work is defined as the product of the force and the displacement in the direction of the force. Since centripetal force is always directed toward the center of the circle and is perpendicular to the velocity of the object, it does not do work on the object because the displacement is zero in the direction of the force. This addresses part (c) of the question, confirming that the work done by the centripetal force is zero because the centripetal force is perpendicular to the velocity of the object in motion.

Answer 2

The correct answer is (c): "The centripetal force is perpendicular to the velocity." This is why the work done by the centripetal force is zero in uniform circular motion.

The work done by a force on an object is defined as the product of the force and the displacement of the object in the direction of the force. Mathematically, it's expressed as
`\( W = \vec{F} \cdot \vec{d} \), where \( \vec{F} \)` is the force vector and
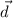`\( \vec{d} \)` is the displacement vector.

When an object moves in a circle at constant speed, the work done by the centripetal force is indeed zero. Let's analyze each of the given options to understand why:

Option (a): "The displacement for each revolution is zero."

- For a single revolution, the object returns to its starting point, so the net displacement over a complete revolution is zero. However, the work done by a force is considered over infinitesimally small displacements along the path, not the net displacement after a complete path.

Option (b): "The average force for each revolution is zero."

- The centripetal force is not zero; it's continuously acting towards the center of the circle to keep the object in circular motion. Its magnitude is constant for uniform circular motion.

Option (c): "The centripetal force is perpendicular to the velocity."

- This is the correct reason. In circular motion at constant speed, the centripetal force is always directed towards the center of the circle, which is perpendicular to the instantaneous velocity of the object at any point on its path. Since the force is perpendicular to the displacement at every point, the work done by the centripetal force is zero.

Option (d): "The magnitude of the acceleration is zero."

- This is incorrect. The object does experience an acceleration, known as centripetal acceleration, which is always directed towards the center of the circle. The magnitude of this acceleration is not zero; it's given by
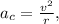`\( a_c = (v^2)/(r) \),` where v is the speed and r is the radius of the circle.