Question

A motor travels 10 mph in still water. The boat takes 4 hours longer to travel 48 miles going upstream than it does to travel 24 miles going downstream. Find the rate of the current.

Answer 1

The rate of the current is 2 mph.

Explanation:

When the boat travels upstream we have:

`v_{T_(1)} = v_(b) - v_(c)`

`(x_(1))/(t_(1)) = v_(b) - v_(c)`

Where:

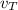`v_(T)`: is the total speed

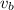`v_(b)`: is the speed of the boat = 10 mph

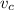`v_(c)`: is the speed of the current

x: is the distance

t: is the time

And when the boat travel downstream we have:

`v_{T_(2)} = v_(b) + v_(c)`

`(x_(2))/(t_(2)) = v_(b) + v_(c)`

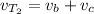
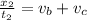
Since the boat takes 4 hours longer to travel 48 miles going upstream than it does to travel 24 miles going downstream we have:

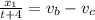`(x_(1))/(t + 4) = v_(b) - v_(c)` (1)

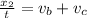`(x_(2))/(t) = v_(b) + v_(c)` (2)

By adding equation (1) with (2):

`(x_(1))/(t + 4) + (x_(2))/(t) = 2v_(b)`

`tx_(1) + (t+4)x_(2) - 2v_(b)t(t+4) = 0`

`48t + 24(t+4) - 2*10t(t+4) = 0`

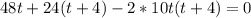
By solving the above equation for t we have:

t = 2 h

Now, by entering "t" into equation (2) we have:

`(24 miles)/(2 h) = 10 mph + v_(c)`

`v_(c) = 2 mph`

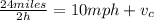
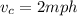
Therefore, the rate of the current is 2 mph.

I hope it helps you!