Question

Please help me out with this question

Answer 1

Answer: (7, 7)

Step-by-step explanation: You have two points so you can take their slope. Slope formula = rise/run. You rise 6 and run 5. So your slope = 6/5. Using (1, 2) as your new starting point, you can use the slope to find L. So rise 6 and run 5, and you will get (7, 7). Hope that helps!

Answer 2

(7, 7)

Explanation:

We can solve for the coordinates of point L by:

• finding the translation vector from point J to point K
• adding the vector to point K to get point L

First, we can find the translation vector from J to K by subtracting the x- and y-coordinates of J from those of K:

`\text{translation} = \langle x_2 - x_1, \ y_2 - y_1 \rangle \text{ for the points } (x_1,y_1) \text{ and } (x_2, y_2)`

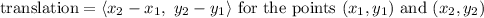
↓ plugging in the coordinates for
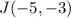`J(-5,-3)` and
`K(1, 2)`

`\text{translation} = \langle 1 - (-5), \ 2 - (-3) \rangle`

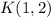
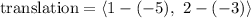
↓ rewriting subtraction of a negative as addition

`\text{translation} = \langle 1 + 5, \ 2 + 3 \rangle`

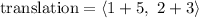
↓ executing the addition

`\text{translation} = \langle 6, \ 5 \rangle`

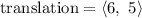
Now, we can add this translation vector to point K:

`\text{ } K(1,\, 2) \\ \underline{+ \ \, \langle 6, \, 5 \rangle} \\ \text{ } \ L(7, 7)`

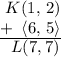
So, the coordinates of point L are (7, 7).