Question

Find the M.A.D. for the following data set.

12, 13, 17, 18, 11, 13, 14
A 14
B 4
C 2
D 62

Answer 1

The **Mean Absolute Deviation (M.A.D.)** is a measure of the variability of a set of data. It is calculated by finding the average distance between each data point and the mean of the data set ¹⁶.

To calculate the M.A.D. for the given data set, we first need to find the mean of the data set:

```

Mean = (12 + 13 + 17 + 18 + 11 + 13 + 14) / 7

= 98 / 7

= 14

```

The mean of the data set is **14**.

Next, we need to find the absolute deviation of each data point from the mean:

```

|12 - 14| = 2

|13 - 14| = 1

|17 - 14| = 3

|18 - 14| = 4

|11 - 14| = 3

|13 - 14| = 1

|14 - 14| = 0

```

Now, we need to find the average of these absolute deviations:

```

M.A.D. = (2 + 1 + 3 + 4 + 3 + 1 + 0) / 7

= **2**

```

Therefore, the M.A.D. for the given data set is **2** ¹⁶.

I hope this helps!

Answer 2

C. 2

Explanation:

The mean absolute deviation (MAD) is a measure of how spread out a data set is. It is calculated by finding the average of the absolute values of the deviations from the mean.

To find the MAD for the data set {12, 13, 17, 18, 11, 13, 14}, we first need to find the mean. The mean is 14.

`\sf mean = (12 + 13 + 17 + 18 + 11 + 13 + 14)/(7) = 14`

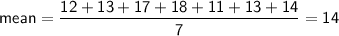
Next, we need to find the absolute deviations from the mean for each data point.

|12 - 14| = 2

|13 - 14| = 1

|17 - 14| = 3

|18 - 14| = 4

|11 - 14| = 3

|13 - 14| = 1

|14 - 14| = 0

Finally, we can find the MAD by averaging the absolute deviations from the mean.

`\sf MAD =( 2 + 1 + 3 + 4 + 3 + 1 + 0)/(7)= 2`

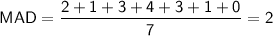
Therefore, the MAD for the data set {12, 13, 17, 18, 11, 13, 14} is C. 2.

Note:

The MAD is a more robust measure of spread than the standard deviation because it is not affected by outliers. Outliers are data points that are much larger or smaller than the other data points in a set. The standard deviation is sensitive to outliers, but the MAD is not.