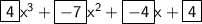Question

What is the product of 4x^2 + x − 2 and x − 2 ?

Enter your answer in simplest form by filling in the boxes.

product = [ ] x^3 + [ ] x^2 + [ ] x + [ ]

NCVA please help

Answer 1

`\sf \boxed{\sf 4} x^3 +\boxed{\sf - 7}x^2 + \boxed{\sf - 4} x + \boxed{\sf 4 }`

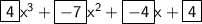
Explanation:

In order to find the product of the polynomials 4x² + x - 2 and x - 2, we can use the distributive property.

Distributive Property:

We distribute each term from the first polynomial 4x² + x - 2 to each term in the second polynomial x - 2, and then add like terms:

`&\sf (4x^2 + x - 2) \cdot (x - 2)\\\\ &\sf = 4x^2 \cdot (x - 2) + x \cdot (x - 2) - 2 \cdot (x - 2)`

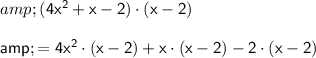
Now, perform the multiplications:

`\sf 4x^2 \cdot (x - 2) = 4x^3 - 8x^2`

`\sf x \cdot (x - 2) = x^2 - 2x`

`\sf -2 \cdot (x - 2) = -2x + 4`

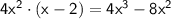
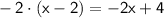
Now, combine the like terms:

`\sf (4x^3 - 8x^2) + (x^2 - 2x) + (-2x + 4)`

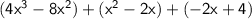
Combine the terms with the same exponent:

`\sf 4x^3 - 8x^2 + x^2 - 2x - 2x + 4`

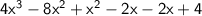
Now, simplify further by combining like terms:

`\sf 4x^3 - 7x^2 - 4x + 4`

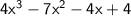
So, the product of 4x² + x - 2 and x - 2 is:

`\sf \boxed{\sf 4} x^3 +\boxed{\sf - 7}x^2 + \boxed{\sf - 4} x + \boxed{\sf 4 }`