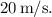The pitching speed of the ball is
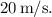
To find the pitching speed of the ball, we can use the following kinematic equation for projectile motion:
![\[ h = (1)/(2) g t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/2lvvyobywy8bivsbbpehpeigecl2pahmue.png)
where:
- h is the initial vertical displacement (4.9 m, the height of the tower),
- g is the acceleration due to gravity (9.8 m/s²),
- t is the time of flight.
We can rearrange this equation to solve for t:
![\[ t = \sqrt{(2h)/(g)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/46p9ajv3pmfsfi267dk2zmiehxchorqes7.png)
Substitute the given values:
![\[ t = \sqrt{\frac{2 * 4.9 \, \text{m}}{9.8 \, \text{m/s}^2}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/mexnh4yx3mhy7ehyfw6n8ok072aan7elnq.png)
![\[ t = √(1) \, \text{s} = 1 \, \text{s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/gkt2fhq2m2heyd6mz3tg7101j3i643ger5.png)
Now, we can use the formula for horizontal displacement in projectile motion:
![\[ \text{Range} = v_0 \cos(\theta) * t \]](https://img.qammunity.org/2024/formulas/physics/high-school/vvf45jguaqs150kl9yofxq13tstw9wuy3d.png)
where:
- Range is the horizontal distance (20 m),
-
 is the initial velocity (pitching speed),
is the initial velocity (pitching speed),
-
 is the angle of projection (assumed to be horizontal),
is the angle of projection (assumed to be horizontal),
- t is the time of flight.
Rearrange the formula to solve for
 :
:
![\[ v_0 = \frac{\text{Range}}{t} \]](https://img.qammunity.org/2024/formulas/physics/high-school/zdf1icmmw352ewqk51650ag6qimq85denm.png)
Substitute the known values:
![\[ v_0 = \frac{20 \, \text{m}}{1 \, \text{s}} = 20 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pb95a1uja3kp6xaw45mcfiduc501bzvydw.png)
Therefore, the pitching speed of the ball is