Question

If he was the midpoint of AC and AC equals 16 what is the value of x when a b equals 2x + 4

Answer 1

x = 2

Explanation:

If point B is the midpoint of segment AC, and the length of AC is 16 units, then the distance from A to B is equal to the distance from B to C, and each of these distances is half of the total length AC.

So, if AB = BC and AC = 16:

`\sf AB = BC = (AC )/(2 )=( 16 )/(2) = 8 units`

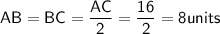
Now, we mentioned that AB equals 2x + 4 units.

Since we've already determined that AB is 8 units, we can set up the equation:

`\sf 2x + 4 = 8`

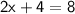
Subtract 4 on both sides:

`\sf 2x + 4-4 = 8-4`

`\sf 2x= 4`

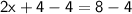
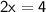
Divide both sides by 2.

`\sf(2 x)/(2) =( 4)/( 2)`

`\sf x = 2`

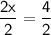
So, the value of x is 2.