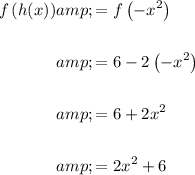Question

Determine the composite functions if ƒ (kx) = 6 - 2x, g(x) = 2, and h(x) = -x². Rewrite your composite in expanded form. A. f(g(x)) = B. g (f (x)) = C. h (f(x)) = = D. g (g(x)) = E. ƒ (ƒ (x)) = F. f(h(x)) =​

Answer 1

`\textsf{A)}\quad f\left(g(x)\right)=6-x`

`\textsf{B)}\quad g\left(f(x)\right)=3-x`

`\textsf{C)}\quad h\left(f(x)\right)=-4x^2+24x-36`

`\textsf{D)}\quad g\left(g(x)\right)=(x)/(4)`

`\textsf{E)}\quad f\left(f(x)\right)=4x-6`

`\textsf{F)}\quad f\left(h(x)\right)=2x^2+6`

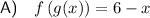
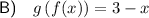
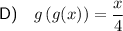
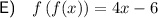
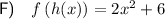
Explanation:

Given functions:


`f(x)=6-2x`

`g(x)=(x)/(2)`

`h(x)=-x^2`

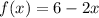
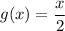
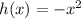
A) To determine the composite function f(g(x)), substitute function g(x) in place of the variable x in function f(x):

`\begin{aligned}f\left(g(x)\right)&=f\left((x)/(2)\right)\\\\&=6-2\left((x)/(2)\right)\\\\&=6-x\end{aligned}`

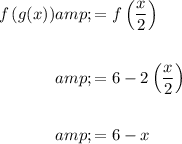
B) To determine the composite function g(f(x)), substitute function f(x) in place of the variable x in function g(x):

`\begin{aligned}g\left(f(x)\right)&=g\left(6-2x\right)\\\\&=((6-2x))/(2)\\\\&=3-x\end{aligned}`

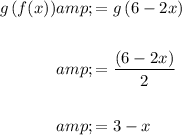
C) To determine the composite function h(f(x)), substitute function f(x) in place of the variable x in function h(x):

`\begin{aligned}h\left(f(x)\right)&=h\left(6-2x\right)\\\\&=-(6-2x)^2\\\\&=-(6-2x)(6-2x)\\\\&=-(36-24x+4x^2)\\\\&=-4x^2+24x-36\end{aligned}`

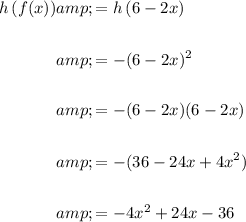
D) To determine the composite function g(g(x)), substitute function g(x) in place of the variable x in function g(x):

`\begin{aligned}g\left(g(x)\right)&=g\left((x)/(2)\right)\\\\&=(\left((x)/(2)\right))/(2)\\\\&=(x)/(4)\end{aligned}`

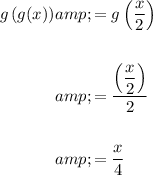
E) To determine the composite function f(f(x)), substitute function f(x) in place of the variable x in function f(x):

`\begin{aligned}f\left(f(x)\right)&=f\left(6-2x\right)\\\\&=6-2\left(6-2x\right)\\\\&=6-12+4x\\\\&=4x-6\end{aligned}`

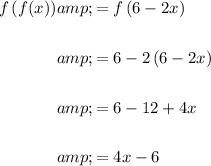
F) To determine the composite function f(h(x)), substitute function h(x) in place of the variable x in function f(x):

`\begin{aligned}f\left(h(x)\right)&=f\left(-x^2\right)\\\\&=6-2\left(-x^2\right)\\\\&=6+2x^2\\\\&=2x^2+6\end{aligned}`