Question

100 POINTS URGENT

For what value of k will a line whose slope and y-intercept are positive one-digit integers pass through the point (10,73) and (1,k)?

Answer 1

k = 10

Explanation:

The equation of a line in slope-intercept form is given by y = mx + b, where m is the slope and b is the y-intercept.

The slope (m) of a line is determined by dividing the difference in y-values by the difference in x-values. Therefore, the slope (m) of a line passing through points (10, 73) and (1, k) is:

`m=(y_2-y_1)/(x_2-x_1)=(k-73)/(1-10)=-(k-73)/(9)=(73-k)/(9)`

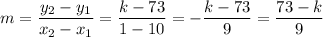
So, the equation of the line in terms of k is:

`y= \left((73-k)/(9)\right)x+b`

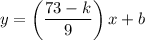
To find an expression for b, substitute point (1, k) into the equation and isolate b:

`k= \left((73-k)/(9)\right)+b`

`b=k- \left((73-k)/(9)\right)`

`b=(9k-73+k)/(9)`

`b=(10k-73)/(9)`

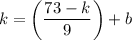
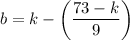
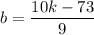
Since the y-intercept (b) must be a positive one-digit integer, this means that (10k - 73) must be a multiple of 9 that is equal to or less than 81.

Multiples of 9 up to an including 81 are:

• 9, 18, 27, 36, 45, 54, 63, 81

To ensure b is a positive one-digit integer, we can only consider multiples of 9 that, when added to 73, yield a multiple of 10. The only suitable multiple within the range is 27.

Therefore, to find the value of k we can set (10k - 73) equal to 27 and solve for k:

`10k-73=27`

`10k=100`

`k=10`

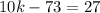
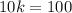
Therefore, the value of k is 10.

To check, substitute k = 10 into the expression for the slope (m):

`m=(73-10)/(9)=(63)/(9)=7`

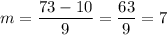
Substitute k = 10 into the expression for the y-intercept (b):

`b=(10(10)-73)/(9)=(100-73)/(9)=(27)/(9)=3`

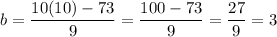
Therefore, the value of k for which a line whose slope and y-intercept are positive one-digit integers passes through the points (10, 73) and (1, k) is:

`\Large\boxed{\boxed{k=10}}`

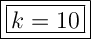
The equation of the line is y = 7x + 3.