Question

Use quadrilateral ABCD with A(1, 5), B(2, 6), C(3, 3) and D(1, 3) and its transformation A'B'C'D' with A'(-3, 1), B'(0, 4), C'(3, -5) and D'(-3, -5). What is the scale factor of the transformation

Answer 1

The scale factor that transforms quadrilateral ABCD to quadrilateral A'B'C'D' is 3

Explanation:

Quadrilateral ABCD has the following coordinates

A(1, 5), B(2, 6), C(3, 3) and D(1, 3)

The image A'B'C'D' has the following coordinates;

A'(-3, 1), B'(0, 4), C'(3, -5), D'(-3, -5)

The length of segment
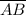`\overline {AB}` = √((2 - 1)² + (6 - 5)²) = √2

The length of segment
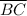`\overline {BC}` = √((3 - 6)² + (3 - 2)²) = √10

The length of segment
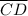`\overline {CD}` = √((1 - 3)² + (3 - 3)²) = 2

The length of segment
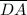`\overline {DA}` = √((1 - 1)² + (3 - 5)²) = 2

For quadrilateral, we have;

A'(-3, 1), B'(0, 4), C'(3, -5), D'(-3, -5)

The length of segment
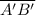`\overline {A'B'}` = √(0 - (-3))² + (4 - 1)²) = 3·√2

The length of segment
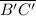`\overline {B'C'}` = √((3 - 0)² + (-5 - 4)²) = 3·√10

The length of segment
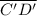`\overline {C'D'}` = √((-3) - 3)² + (-5 - (-5))²) = 6

The length of segment
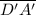`\overline {D'A'}` = √((-3) - (-3))² + ((-5) - 1)²) = 6

The scale factor that transforms quadrilateral ABCD to A'B'C'D' is given as follows;

`The \, scale \, factor \, of \, transformation = \frac{\overline {A'B'}}{\overline {AB}} = \frac{\overline {B'C'}}{\overline {BC}} = \frac{\overline {C'D'}}{\overline {CD}} = \frac{\overline {D'A'}}{\overline {DA}} = 3`

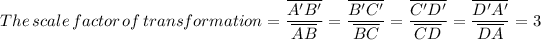
Therefore, the scale factor that transforms quadrilateral ABCD to A'B'C'D' = 3