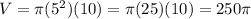Question

A cube of ice has edges of length 10. What is the volume of the largest cylinder that can be carved from the cube? a. 500π cubic units b. 250π cubic units c. 100π cubic units d. 50π cubic units

Answer 1

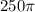`250\pi` cubic units

Explanation:

Interesting question! Can you visualize a cylinder sitting inside a box? And the cylinder is the maximum size such that it's touching the box on all 6 faces?

Then how wide is that cylinder? It's exactly as wide as the box, right? Which we know is 10 units.

That's how big of a circle you could lay flat in that box, so let's start by finding the area of that circle:

`A = \pi r^(2)`

We don't have the radius r directly, but we do have the diameter d, which is 10 units. Now, they always say if you know d but not r, then use this formula:

A =
`\pi (d/2)^(2) = \pi d^(2)/4^(2)`

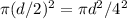
But that's so messy, why not just divide d by 2 at the beginning to get r, and then use r directly in the equation?

diameter = 10, so radius is half of that, or 5. So now we know r:

A =
`\pi r^(2)`

`A = \pi 5^(2) = 25\pi`

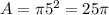
But that's the area of the base of the cylinder we're looking for.

Now we have to multiply that by the height of the cylinder to find its volume, right?

`V = \pi r^(2)h` (Which btw, you could express as A·h, so: V = Ah)

`\pi r^(2)` is the area term, which we already calculated to be
`25\pi`.

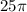So what's the maximum height of this cylinder sitting inside a box of side 10? The most it can be is 10, right? So h = 10, and:

`V = Ah = 25\pi (10) = 250\pi`

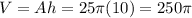
Or if you want to start from the beginning:

`V = \pi r^(2)h`

`V = \pi (5^(2))(10) = \pi (25)(10) = 250\pi`