Question

Divide algebraic expression:
5x³+14x²+7x-2/(5x²+4x-1)

Answer 1

x + 2

Explanation:

`(5x^3+14x^2+7x-2)/(5x^2+4x-1)`

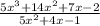
Factor the denominator.

`(5x^3+14x^2+7x-2)/((x+1)(5x-1))`

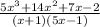
Check if -1 or 1/5 are roots of the numerator.

`5(-1)^3+14(-1)^2+7(-1)-2=0\\5((1)/(5))^3+14((1)/(5))^2+7((1)/(5))-2=0`

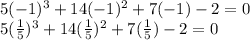
x+1 and 5x−1 are both factors of the numerator. Use grouping to factor out x+1 from the numerator:

`5x^3+14x^2+7x-2\\5x^3+5x^2+9x^2+7x-2\\5x^2 (x+1)+(x+1)(9x-2)\\(x+1)(5x^2+9x-2)\\(x+1)(5x-1)(x+2)`

Therefore, the algebraic expression divides to x + 2.