Question

The exponential model A = 608.4e^0.028 describes the population, A, of a country in millions, t years after 2003. Use the model to determine when the population of the country will be 700 million.

Answer 1

the population is projected to reach 700 million around the year 2015.

Explanation:

To determine when the population of the country will be 700 million, you can set up the equation using the given exponential model:

`A = 608.4e^(0.028t)`

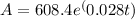
You want to find the time (t) when the population (A) is 700 million. So, you can rewrite the equation as:

`700 = 608.4e^(0.028t)`

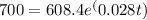
Now, you need to solve for t. First, divide both sides by 608.4 to isolate the exponential term:

`e^(0.028t) = 700 / 608.4`

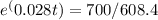
Now, take the natural logarithm (ln) of both sides to solve for t:

`ln(e^(0.028t)) = ln(700 / 608.4)`

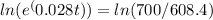
The natural logarithm and exponential functions are inverse operations, so
`ln(e^(0.028t))` simplifies to just 0.028t:

`0.028t = ln(700 / 608.4)`

Now, divide both sides by 0.028 to solve for t:

`t = ln(700 / 608.4) / 0.028`

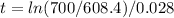
Use a calculator to compute this value:

t ≈ 12.18 years

So, the population of the country is projected to reach 700 million approximately 12.18 years after 2003. To find the year, add 12.18 to 2003:

Year ≈ 2003 + 12.18 ≈ 2015.18

Rounded to the nearest year, the population is projected to reach 700 million around the year 2015.