Question

You want to buy a car. The loan amount will be $28,000. The company is offering a 5% interest rate for 60 months (5 years). What will your monthly payments be?

​

Answer 1

$510.28.

Explanation:

To calculate your monthly payments on a car loan, you can use the formula for calculating the monthly payment on a fixed-rate loan. The formula is:

`\[PMT = (P \cdot r \cdot (1+r)^n)/((1+r)^n-1)\]`

Where:

-
`\(PMT\)` is the monthly payment.

-
`\(P\)` is the principal loan amount ($28,000 in this case).

-
`\(r\)` is the monthly interest rate, which is the annual interest rate divided by 12 and expressed as a decimal.

-
`\(n\)` is the number of monthly payments, which is the loan term in years multiplied by 12.

In this case, you have:

-
`\(P = $28,000\)`

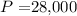
- Annual interest rate = 5%

- Loan term = 5 years

First, calculate the monthly interest rate
`(\(r\))` by dividing the annual interest rate by 12:

`\[r = (5\%)/(12) = 0.05 / 12 = 0.0041667\]`

Next, calculate the number of monthly payments
`(\(n\))`:

`\[n = 5 years * 12 months/year = 60 months\]`

Now, plug these values into the formula:

`\[PMT = (28000 \cdot 0.0041667 \cdot (1+0.0041667)^(60))/((1+0.0041667)^(60)-1)\]`

Let's calculate this using a calculator:

`\[PMT \approx (28000 \cdot 0.0041667 \cdot (1.0041667)^(60))/((1.0041667)^(60)-1)\]`

`\[PMT \approx (28000 \cdot 0.0041667 \cdot 1.2766563)/(1.2766563-1)\]`

Now, calculate the value in the numerator:

`\[28000 \cdot 0.0041667 \cdot 1.2766563 \approx 141.26\]`

And in the denominator:

`\[1.2766563 - 1 \approx 0.2766563\]`

Finally, divide the numerator by the denominator:

`\[PMT \approx (141.26)/(0.2766563) \approx $510.28\]`

So, your monthly car payment will be approximately $510.28.