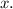Answer:
f ′ (x)=3.99x 2 +7.98x+45.06
Explanation:
Let's break down the process of finding the derivative of the function
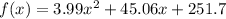 in simpler terms.
in simpler terms.
We want to find the derivative
 , which tells us how the function's value changes as
, which tells us how the function's value changes as
 changes. It's like finding the slope of the function at any point.
changes. It's like finding the slope of the function at any point.
1. Start with the function

2. We'll use a formula to calculate the derivative. This formula looks at how the function changes when we make a tiny change in
 , which we'll call
, which we'll call
 . The formula is:
. The formula is:
![\[f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2g4vw7sva28unvr9yrnj5l0v1i4vf65k6b.png)
In plain terms, it means: "Find the difference in
 when
when
 changes by a very small amount
changes by a very small amount
 and divide it by that small amount
and divide it by that small amount
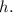 "
"
3. Plug our function \(f(x)\) into the formula:
![\[f'(x) = \lim_(h \to 0) (3.99(x + h)^2 + 45.06(x + h) + 251.7 - (3.99x^2 + 45.06x + 251.7))/(h)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k4ophxujgcbezxhcplh7wellrxrjkf4lej.png)
This represents the change in
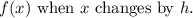
4. Simplify the expression inside the limit:
![\[f'(x) = \lim_(h \to 0) (3.99x^2 + 7.98xh + 3.99h^2 + 45.06h)/(h)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2j6prbjlvtunpeqpxq5vuxrmnko4szh0iu.png)
This breaks down how
 changes when
changes when
 changes by
changes by
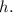
5. Cancel out \(h\) in the numerator and denominator:
![\[f'(x) = \lim_(h \to 0) (3.99x^2 + 7.98x + 3.99h + 45.06)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hjdx5gptw5ww32em3fn59pp18hsh1ubzw7.png)
This tells us the rate of change of
 as
as
 gets smaller and smaller.
gets smaller and smaller.
6. Finally, as
 approaches 0 (gets extremely small), the term
approaches 0 (gets extremely small), the term
 and
and
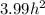 become very close to 0. So, we're left with:
become very close to 0. So, we're left with:
![\[f'(x) = 3.99x^2 + 7.98x + 45.06\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w5gdgu9iza5emnj26h4ovkuw1pbzrq1nti.png)
This is the derivative
 of the original function. It represents how the original function's value changes with respect to
of the original function. It represents how the original function's value changes with respect to