Question

A triangle vertices (2,-3),(-2,1) and (1,2). Are any of the sides congruent

Answer 1

Answer: No.

Explanation:

We can use the distance formula to find the distance of one side.

`\displaystyle d=\sqrt{(x_(2)-x_(1))^2 +(y_(2)-y_(1))^2} \rightarrow d=√((-2-2)^2+(1--3)^2) \rightarrow d=√(32)`

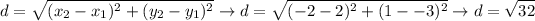
Now, we will find another side.

`\displaystyle d=\sqrt{(x_(2)-x_(1))^2 +(y_(2)-y_(1))^2} \rightarrow d=√((1-2)^2+(2--3)^2) \rightarrow d=√(26)`

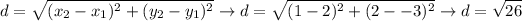
Lastly, we will find the third side.

`\displaystyle d=\sqrt{(x_(2)-x_(1))^2 +(y_(2)-y_(1))^2} \rightarrow d=√((-2-1)^2+(1-2)^2) \rightarrow d=√(10)`

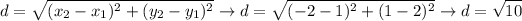
No. 32 ≠ 26 ≠ 10. None of these sides are congruent. I have attached a graph of these vertices. See attached.