Answer:
So, at
 , the function
, the function
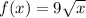 is changing at a rate of
is changing at a rate of
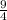 , which means it's increasing or decreasing at that rate at that particular point.
, which means it's increasing or decreasing at that rate at that particular point.
Explanation:
Certainly! To find the instantaneous rate of change of the function
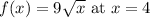 , think of it as how fast the function is changing at that specific point.
, think of it as how fast the function is changing at that specific point.
1. Start with the function
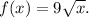
2. Find the derivative
 of this function, which tells you how fast it's changing at any
of this function, which tells you how fast it's changing at any
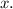
3. The derivative
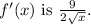 This formula describes how the rate of change depends on the value of
This formula describes how the rate of change depends on the value of
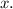
4. Now, plug in the specific
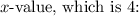
![\[f'(4) = (9)/(2√(4))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7hsmy0lxiuut1iczio5x15e5f7ryurq1xh.png)
5. Simplify the expression:
![\[f'(4) = (9)/(2 \cdot 2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6cztj0588lrhkzs74jxm4cjhsd3kds3y2o.png)
![\[f'(4) = (9)/(4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5pk2lqw19nd37htk3r6q8i0eupobzl2q4q.png)
So, at
 , the function
, the function
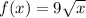 is changing at a rate of
is changing at a rate of
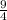 , which means it's increasing or decreasing at that rate at that particular point.
, which means it's increasing or decreasing at that rate at that particular point.