Answer:
So, the maximum temperature rise
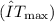 due to viscous dissipation is 0.25 degrees Celsius.
due to viscous dissipation is 0.25 degrees Celsius.
Step-by-step explanation:
To estimate the maximum temperature of the oil due to viscous dissipation in Couette flow, we can use the energy equation for steady-state flow, which takes into account both conduction and viscous dissipation. The energy equation for this situation is:
![\[q = (kA)/(d) \Delta T + \mu \cdot \frac{{du^2}}{dy^2}\]](https://img.qammunity.org/2024/formulas/physics/college/18imelnie5ezhvtr27mkjvej7o2han6vd2.png)
Where:
- \(q\) is the heat transfer rate per unit area.
- \(k\) is the thermal conductivity of the fluid (0.2 W/m·K).
- \(A\) is the cross-sectional area of the plates.
- \(d\) is the distance between the plates (0.1 mm = 0.0001 m).
- \(\Delta T\) is the temperature difference between the plates.
- \(\mu\) is the dynamic viscosity of the fluid (0.2 Pa·s).
- \(u\) is the velocity of the upper plate (5 m/s).
- \(y\) is the distance from the lower plate.
First, let's calculate the temperature difference
 :
:
Now, let's calculate the heat transfer rate per unit area
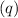 due to viscous dissipation. We'll consider the upper plate to be at a higher temperature due to viscous dissipation:
due to viscous dissipation. We'll consider the upper plate to be at a higher temperature due to viscous dissipation:
![\[q = \mu \cdot \frac{{du^2}}{dy^2}\]](https://img.qammunity.org/2024/formulas/physics/college/foc4c10bcncrb6rla2zqt9hu4uf7mrrva8.png)
Since we want to estimate the maximum temperature,
![\[\Delta T = T_{\text{upper}} - T_{\text{lower}} = 30°C - 30°C = 0K\]](https://img.qammunity.org/2024/formulas/physics/college/mz9pxopo59j29tzw67mxwp9kgfo45xhork.png)
we need to find the maximum value of
 , which occurs at
, which occurs at
 . The derivative
. The derivative
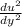 is maximized at
is maximized at
 for Couette flow.
for Couette flow.
![\[(du^2)/(dy^2) = (d)/(dy)(du^2/dy) = 0\]](https://img.qammunity.org/2024/formulas/physics/college/o0ys5eqmwvklrjr8unnb32tpzw7l1o6eum.png)
So,
 is maximized at
is maximized at
 , and we can calculate it there:
, and we can calculate it there:
![\[q_{\text{max}} = \mu \cdot \frac{{du^2}}{dy^2} \bigg|_(y=0)\]](https://img.qammunity.org/2024/formulas/physics/college/hon23epn0a1r4s893i6lo5bt8o3c0ngyri.png)
Now, plug in the known values:
![\[q_{\text{max}} = (0.2 Pa·s) \cdot \frac{{(5 m/s)^2}}{0.0001 m^2} = 500,000 W/m^2 = 500 kW/m^2\]](https://img.qammunity.org/2024/formulas/physics/college/q2j3awj3egf3s4szh4sc33b93fjoij6s4f.png)
Now, let's calculate the maximum temperature rise
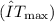 due to this heat transfer using the formula:
due to this heat transfer using the formula:
![\[q_{\text{max}} = (kA)/(d) \cdot ΔT_{\text{max}}\]](https://img.qammunity.org/2024/formulas/physics/college/5wnsbo546ecwy81ssspwvmdqr4y9ucys4x.png)
Rearrange the formula to solve for
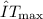 :
:
![\[ΔT_{\text{max}} = \frac{q_{\text{max}} \cdot d}{kA}\]](https://img.qammunity.org/2024/formulas/physics/college/tcdt95aqrglrp0ncrbvt4ozn7asdmkfi8d.png)
Now, plug in the values:
![\[ΔT_{\text{max}} = ((500 kW/m^2) \cdot 0.0001 m)/(0.2 W/m·K \cdot A)\]](https://img.qammunity.org/2024/formulas/physics/college/rz1iqn7i5rndus43cnstoi5j0g1wszdqgs.png)
The value of
 depends on the geometry of your plates. Assuming a unit width (1 m) and considering only one plate (as the other one is stationary), we have
depends on the geometry of your plates. Assuming a unit width (1 m) and considering only one plate (as the other one is stationary), we have
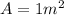 .
.
![\[ΔT_{\text{max}} = ((500 kW/m^2) \cdot 0.0001 m)/(0.2 W/m·K \cdot 1 m^2) = 0.25 K\]](https://img.qammunity.org/2024/formulas/physics/college/pca0w01s1xinu9me2cfhbguactf63pn68u.png)
So, the maximum temperature rise
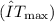 due to viscous dissipation is 0.25 degrees Celsius.
due to viscous dissipation is 0.25 degrees Celsius.