Question

Water, flowing at 2 kg/s through a 40 mm diameter tube that is 4 m long, enters at a temperature of 25 0 C. If the surface temperature of the pipe is 90 0 C, calculate: The outlet temperature of the water

Answer 1

So, the outlet temperature of the water is approximately 92°C.

Step-by-step explanation:

To calculate the outlet temperature of the water, we can use the concept of heat transfer in a pipe. The heat transferred to the water will cause its temperature to rise from the inlet temperature to the outlet temperature.

We can use the following formula for heat transfer:

`\[Q = m \cdot c \cdot \Delta T\]`

Where:

-
`\(Q\)` is the heat transfer (in joules).

-
`\(m\)` is the mass flow rate of water (in kilograms per second).

-
`\(c\)` is the specific heat capacity of water (approximately 4,186 J/(kg·K) at room temperature).

-
`\(\Delta T\)` is the change in temperature (in kelvin or degrees Celsius).

First, let's calculate the heat transfer
`(\(Q\))`.

Given:

- Mass flow rate
`(\(m\))` = 2 kg/s

- Inlet temperature
`(\(T_{\text{inlet}}\)) = 25°C = 25°C + 273.15 (convert to kelvin)`

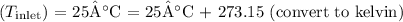
- Surface temperature of the pipe (\(T_{\text{surface}}\)) = 90°C = 90°C + 273.15 (convert to kelvin)

Now, calculate the change in temperature
`(\(\Delta T\))`:

`\[\Delta T = T_{\text{surface}} - T_{\text{inlet}}\]`

`\[\Delta T = (90°C + 273.15 K) - (25°C + 273.15 K) = 365.15 K - 298.15 K = 67 K\]`

Now, calculate the heat transfer
`(\(Q\))`using the formula:

`\[Q = m \cdot c \cdot \Delta T\]`

`\[Q = (2 kg/s) \cdot (4,186 J/(kg·K)) \cdot 67 K = 561,784 J/s = 561,784 W (watts)\]`

Now that we have calculated the heat transfer
`(\(Q\))`, we can use it to find the outlet temperature
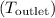`(\(T_{\text{outlet}}\))` using the same formula:

`\[Q = m \cdot c \cdot \Delta T\]`

`\[\Delta T = (Q)/(m \cdot c)\]`

`\[\Delta T = (561,784 J/s)/((2 kg/s) \cdot (4,186 J/(kg·K))) \approx 67 K\]`

Now, add this change in temperature to the inlet temperature to find the outlet temperature:

`\[T_{\text{outlet}} = T_{\text{inlet}} + \Delta T\]`

`\[T_{\text{outlet}} = (25°C + 273.15 K) + 67 K = 365.15 K\]`

Convert the outlet temperature from kelvin to degrees Celsius:

`\[T_{\text{outlet}} = 365.15 K - 273.15 K = 92°C\]`

So, the outlet temperature of the water is approximately 92°C.