Question

The drag force F on a plate of width W and length L due to flow is calculated using the following expression: F = 1.328 VALLW24 Here, p is density of the fluid, y is viscosity of the fluid and u is far field velocity of the fluid. (a) Derive an expression for the friction factor

Answer 1

`\[f = (0.664AL)/(W\\u) \cdot \left((V)/(u)\right)^2\]`

Step-by-step explanation:

To derive an expression for the friction factor, we can start with the definition of the drag force (F) on the plate and then express it in terms of the other variables, including the friction factor (f). The drag force (F) is given as:

`F=1.328*(V^2AL)/(V)`

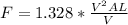
Where:

- \(F\) is the drag force.

- \(V\) is the velocity of the fluid (far field velocity, u).

- \(A\) is the cross-sectional area of the plate (width x length, W x L).

- \(L\) is the length of the plate.

- \(\\u\) is the viscosity of the fluid (y).

Now, let's consider the friction factor (f). The Darcy-Weisbach equation relates the friction factor to other parameters in fluid flow:

`\[F = (4)/(\rho) \cdot (L)/(D) \cdot (1)/(2) \cdot \rho \cdot u^2 \cdot f\]`

Where:

- \(F\) is the drag force.

- \(\rho\) is the density of the fluid (p).

- \(L\) is the length of the plate.

- \(D\) is the characteristic hydraulic diameter (in this case, it's proportional to the width, W).

- \(u\) is the velocity of the fluid (far field velocity, V).

- \(f\) is the friction factor.

Since we're dealing with a plate, the characteristic hydraulic diameter (D) can be approximated as the width (W) of the plate:

`\[D \approx W\]`

Now, we can equate the expressions for the drag force and the Darcy-Weisbach equation:

`\[1.328 \cdot (V^2AL)/(\\u) = (4)/(\rho) \cdot (L)/(W) \cdot (1)/(2) \cdot \rho \cdot u^2 \cdot f\]`

Let's simplify this equation:

`\[(1.328AL)/(W\\u) \cdot V^2 = (2L)/(W) \cdot u^2 \cdot f\]`

Now, we can solve for the friction factor (f):

`\[f = (1.328AL)/(W\\u) \cdot (V^2)/(2L \cdot u^2)\]`

Simplify further:

`\[f = (0.664AL)/(W\\u) \cdot \left((V)/(u)\right)^2\]`

So, the expression for the friction factor (f) is:

`\[f = (0.664AL)/(W\\u) \cdot \left((V)/(u)\right)^2\]`

This is the derived expression for the friction factor in terms of the given variables.