Question

Can someone answer this question WITH the steps please

(ITS THE CHALLENGE QUESTION BTW, THE ONE IN THE RED BOX)

thanks <3

Answer 1

`\huge\boxed{p=0.115, \\ q=0.365, \\ r=0.112}`

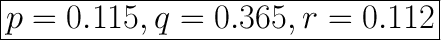
Explanation:

P(not C) is the probability of C not being selected, which in this question, is equivalent to 0.15 + 0.2 + p + q (i.e. the sections not in bubble C).

Hence,

0.83 = 0.15 + 0.2 + p + q.

0.83 = 0.35 + p + q

0.48 = p + q

Thus, this is the first equation in our system:
`\boxed{q+p=0.48}`

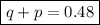
The next equation in our system comes from the fact that P(B) = 2P(A).

P(B) = p + q + 0.05

P(A) = p + 0.15

Thus, 2(p + 0.15) = p + q + 0.05

Distribute "2"

2p + 0.3 = p + q + 0.05

Group like terms

q - p = 0.25

Thus, this is the second equation in our system, and allows us to solve via elimination.

`\boxed{q+p=0.48}\\\boxed{q-p=0.25}`

Adding the 2 equations yields:

`2q = 0.73`

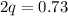
Thus, q = 0.365.

Thus, p = 0.115

Now, because everything in the diagram must sum to 1.00, plug in every value to get:

`\huge\boxed{0.15+0.115+0.365+0.05+0.2+r=1}`

Simplifying, we get:

0.88 + r = 1

Thus, r = 0.12.

Hope that helped and let me know if you want me to elaborate on anything :)