Question

I need the answer right now

Answer 1

`\textsf{Rational numbers are:}\sf 0.329, 127.5 \textsf{ and }-89`

`\textsf{Irrational numbers are:}\sf √(101)`

Explanation:

A rational number is a number that can be expressed as a fraction of two integers, where the denominator is not equal to zero.

Examples of rational numbers include:

• 
  `\sf (1)/(2)`
• 
  `\sf (5)/(2)`
• 
  `\sf (-15)/(4)`
• 0.5
• 1.3333... (repeating decimal)

An irrational number is a number that cannot be expressed as a fraction of two integers.

Examples of irrational numbers include:

• 
  `\sf √(2)`
• 
  `\sf √(3)`
• π
• e
• 0.12345678910111213... (non-repeating decimal)

In this case:

By studying definition and example of rational and irrational number, we can say that:

`\textsf{Rational numbers are:}\sf 0.329, 127.5 \textsf{ and }-89`

`\textsf{Irrational numbers are:}\sf √(101)`

Answer 2

`\textsf{Rational numbers:}\quad \boxed{0.329}\;\;\; \boxed{127.5}\;\;\; \boxed{-89}`

`\textsf{Irrational numbers:}\quad \boxed{√(101)}`

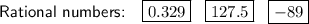
Explanation:

Rational numbers

Rational numbers can be expressed as the quotient of two integers (where the denominator is non-zero) and have finite or repeating decimal representations.

Irrational numbers

Irrational numbers cannot be expressed as fractions and have non-repeating, non-terminating decimal expansions.

`\hrulefill`

0.329 is a rational number because it is a terminating (finite) decimal. It can be expressed as the fraction 329/1000.

127.5 is also a rational number because it is again a terminating (finite) decimal. It can be expressed as the fraction 255/2.

-89 is a rational number since all integers can be expressed as fractions by dividing them by 1. Therefore, -89 can be expressed as the fraction -89/1.

√(101) is an irrational number. This is because 101 is a prime number, and its square root results in a non-repeating, non-terminating decimal, making it impossible to express as a fraction.