Question

the base of 12-foot ladder is 2 feet from a building. if the ladder reaches the flat roof, how tall is the building? give the height of the building as a simplified radical and as a decimal rounded to the tenths place.

Answer 1

answer:
2 squared + x squared = 12 squared.
4+ x squared= 144
square root of x squared = square root of 140
x = 11.8 and 2squareroot of 35

Answer 2

The height of the building, we can use the Pythagorean theorem. By substituting the values into the equation, we can solve for the height and simplify radical and approximately 11.8 feet as a decimal rounded to the tenths place.

We can use the Pythagorean theorem to solve this problem. The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In this case, the ladder forms a right-angled triangle with the building. Let h be the height of the building, b be the distance from the base of the ladder to the building, and l be the length of the ladder. According to the Pythagorean theorem:

`h^2 + b^2 = l^2`

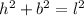
Given that the length of the ladder (l) is 12 feet, and the distance from the base of the ladder to the building (b) is 2 feet, we can substitute these values into the equation:

`h^2 + 2^2 = 12^2`

Solving for h:

`h^2 + 4 = 144`

`h^2 = 140`

`h = √(140)`

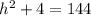
Now, we can simplify
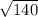`√(140)` aculate its decimal approximation:

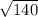`√(140)` ≈ 11.8

Therefore, the height of the building is
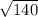`√(140)` a simplified radical and approximately 11.8 feet as a decimal rounded to the tenths place.