Question

imagine two cars are at rest 15 miles apart. at noon, car a starts heading toward car b with a speed of 10 mph. at an unknown time on the clock, car b starts heading towards car a with a speed of 25 mph. if the two cars meet at 1 pm determine the time on the clock when car b started moving

Answer 1

`12\!:\!48\; \text{pm}`.

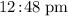Step-by-step explanation:

Consider how fast the distance between the two vehicles is changing:

• When only vehicle A is moving, the distance between A and B reduces at a rate of
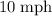  `10\; \text{mph}` (same as the speed of A relative to the ground.)
• When both vehicles are moving, the distance between the two reduces at a rate of
  `(10 + 25)\; \text{mph} = 35\; \text{mph}` (sum of the speed of the two vehicles relative to the ground.)

Let
`x` be the minute when vehicle B started moving. It is given that the two vehicles met one hour after vehicle A started moving.

• For
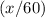  `(x/60)` of the hour, vehicle A has been moving towards vehicle B while B stays stationary.
• After that, for
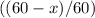  `((60 - x) / 60)` of the hour, both vehicles were moving toward each other.

During the first
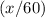`(x/60)` of the hour, the distance between A and B is reduced at a rate of
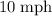`10\; \text{mph}` for
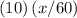`(10)\, (x / 60)` miles in total.

After that, during the
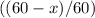`((60 - x) / 60)` of the hour, the distance between A and B is reduced at a rate of
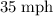`35\; \text{mph}` for
`(35)\, ((60 - x) / 60)` miles in total.

The initial distance between two vehicles was initially
`15` miles. This distance would be equal to the sum of the two sections:
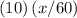`(10)\, (x / 60)` miles, and
`(35)\, ((60 - x) / 60)` miles.

`\displaystyle (10)\, (x)/(60) + (35)\, (60 - x)/(60) = 15`.

`10\, x + 2100 - 35\, x = 900`.

`x = \displaystyle (900 - 2100)/(10 - 35) = 48`.

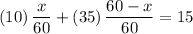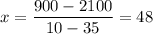In other words, vehicle B started at
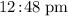`12\!:\!48\; \text{pm}`.