Question

Find the numerical value of the log expression

Answer 1

9

Explanation:

I'm going to solve this question by expanding the logarithm (note that you can also solve this equation by solving for a, b, and c)

We know the following

`log(ab)=log(a)+log(b)`

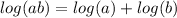
Which means we can split the numerator into

`log(b^(1/2))+log(c^(3/2))`

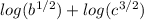
We also know that

`log(a^(x))=x*log(a)`

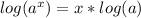
Which means that we can rewrite the following as

`(log(b))/(2)+(3log(c))/(2)`

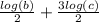
We can evaulate this and get

-1+12= 11

for the numerator

Now we need to take care of the denominator

we know the following

`log((x)/(y))=log(x)-log(y)`

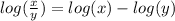
which means that we have

11-2log(a)

solve and get

11-2

9