Question

Find two numbers who have product of 81 and sum of 30

Answer 1

3 & 27

Explanation:

This is going to be a system of equations problem.

We have 2 variables, and we know 2 relationships between them. Let's call the unknown numbers x & y and write those relationships as equations:

• xy = 81
• x + y = 30

Do you understand how I converted the words to those equations? Don't move on until you do.

Now we have to solve that system of equations. To do that:

• Solve one of the equations for one of the variables.
• Substitute that expression into the other equation.
• Find what the other variable equals. It'll be a number.
• Put that number into either equation to find the other variable.

It doesn't matter which equation or which variable you choose.

In this problem, the second one is a little easier to use. Solve for x:

x + y = 30 --> x = -y + 30

Now we have an expression for x in terms of y. If we put that into the other equation, watch what happens:

xy = 81 substitute:

(-y + 30)y = 81

`-y^(2) + 30y = 81`

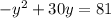
That's starting to look like a quadratic equation, so let's put it in that form:

`-y^(2) + 30y - 81 = 0`

If you use the Quadratic Formula to solve that (there's one at Calculator Soup) you'll find that the two numbers are 3 and 27.

Check our work:

• Do they multiply to 81? Yes.
• Do they sum to 30? Yes

So the answer must be correct.