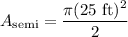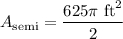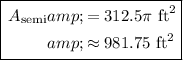Question

Calculate the perimeter and area of the shape round to two decimal places

Answer 1

`P \approx 128.54\text{ ft}`

`A \approx 981.75\text{ ft}^2`

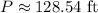
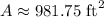
Explanation:

Perimeter

We can construct an equation that models the perimeter of a semicircle with a diameter of 50ft using the formula for the circumference of a circle:

`C_\circ = \pi d`

`\implies P_\text{semi} = \frac{C}2 + d`

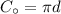
↓ replacing
`C` with its definition

`P_\text{semi} = (\pi d)/(2) + d`

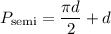
Now, we can solve for the perimeter of the semicircle by plugging in the given diameter (50 ft) and simplifying:

`P_\text{semi} = \frac{\pi (50\text{ ft})}{2} + 50\text{ ft}`

`P_\text{semi} = (25\pi\text{ ft}) + 50 \text{ ft}`

`\boxed{\begin{aligned}P_\text{semi} &= (25\pi + 50)\text{ ft} \\ &\approx 128.54\text{ ft}\end{aligned}}`

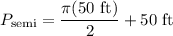
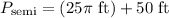
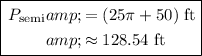
Area

We can construct an equation that models the area of a semicircle with a diameter of 50ft using the formula for the area of a circle:

`A_\circ = \pi r^2`

`\implies A_\text{semi} = (\pi r^2)/(2)`

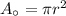
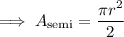
We can solve for the semicircle's radius using the equation:

`r = (d)/(2)`

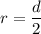
↓ plugging in the given diameter value

`r = \frac{50\text{ ft}}{2}`

`r = 25\text{ ft}`

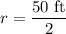
Now, we can solve for the semicircle's area by plugging this radius value into the area equation and simplifying:

`A_\text{semi} = \frac{\pi (25\text{ ft})^2}{2}`

`A_\text{semi}=\frac{625\pi\text{ ft}^2}{2}`

`\boxed{\begin{aligned}A_\text{semi}&=312.5\pi\text{ ft}^2 \\ &\approx981.75\text{ ft}^2\end{aligned}}`