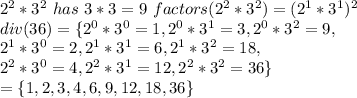Question

What is the sum of all the numbers smaller than 200 that have exactly 9 divisors?

Answer 1

Hi,

332

Explanation:

Let's say n the number that have 9 divisors.
Because there are 9 divisors (a odd number), n must be a square.

15²=225 >200

The maximum should be 14²=196

We are thus looking numbers , product of 2 prime factors with exponent maximum 2.

`2^2*3^2\ has\ 3*3=9\ factors ( 2^2*3^2)=(2^1*3^1)^2\\div(36)=\{2^0*3^0=1,2^0*3^1=3,2^0*3^2=9,\\2^1*3^0=2,2^1*3^1=6,2^1*3^2=18,\\2^2*3^0=4,2^2*3^1=12,2^2*3^2=36\}\\=\{1,2,3,4,6,9,12,18,36\}\\`

`next\ one:\ 2^2*5^2=(2*5)^2=100\\next\ one:\ 2^2*7^2=(14)^2=196\\\\(2*11)^2=481\ : too\ high\\\\(3*5)^2=15^2=225:\ too\ high \\\\The\ sum\ is\ thus:\ 36+100+196=332\\`