Question

I need help so bad its so hard broooooooooooo

Answer 1

• 
  `x = 11°`
• 
  `m∠C = 105°`

Given :

• A llgm ABCD with a pair of opposite angles measuring (-2+7x) and (6x + 9)

To find :

• Value of x
• Measure angle C

Solution :

We know that,

• Opposite angles of a llgm are equal
• m∠D = m∠B
• 6x + 9 = -2 + 7x
• 6x - 7x = -2 -9
• -x = -11
• x = 11

Thus, the value of x = 11.

Also,

• Sum of adjacent angles of a llgm = 180°
• m∠B + m∠C = 180°
• -2 + 7x + m∠C = 180°

Plugging in the value of x

• -2° + 7(11°) + m∠C = 180°
• -2° + 77° + m∠C = 180°
• 75° + m∠C = 180°
• m∠C = 180° -75°
• m∠C = 105°

Thus, m∠C = 105°.

Answer 2

x = 11

m∠C = 105°

Explanation:

From observation of the given diagram, it appears that figure ABCD is a parallelogram.

In a parallelogram, opposite angles are congruent. In parallelogram ABCD, ∠B and ∠D are opposite angles. To find the value of x, we can equate the measures of ∠B and ∠D:

`\begin{aligned}m \angle B &=m \angle D\\-2+7x&=6x+9\\-2+7x-6x&=6x+9-6x\\-2+x&=9\\-2+x+2&=9+2\\x&=11\end{aligned}`

Therefore, x = 11.

Now, to determine the measures of ∠B and ∠D, substitute x = 11 into one of the angle expressions:

`\begin{aligned}m \angle B &=-2+7(11)\\m \angle B &=-2+77\\m \angle B &=75^(\circ)\end{aligned}`

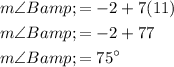
Therefore, m∠B = 75° and m∠D = 75°.

In a parallelogram, adjacent angles are supplementary, which means their sum is 180°. Therefore, to find the measure of angle C, subtract the measure of angle B from 180°:

`\begin{aligned}m \angle C &=180^(\circ)-m \angle B\\m \angle C &=180^(\circ)-75^(\circ)\\m \angle C &=105^(\circ)\end{aligned}`

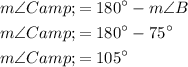
Therefore, m∠C = 105°.