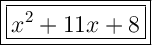Answer this: Let, f(x) = x^2 + 7x - 10 g(x) = x + 2 Solution: \begin{aligned}(f \circ g)(x)& = f(g(x)) \\&= \end{aligned}​

Question

Answer this:

Let,

`f(x) = x^2 + 7x - 10`

`g(x) = x + 2`
Solution:

`\begin{aligned}(f \circ g)(x)& = f(g(x)) \\&= \end{aligned}`​

Answer 1

`(f \circ g)(x)=x^2+11x+8`

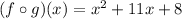
Explanation:

Composite functions are when the output of one function is used as the input of another.

(f o g)(x) is a composite function and can also be written as f(g(x)).

It indicates that the inner function g(x) must be applied before the outer function f(x). So if we had to find (f o g)(2), we would first calculate the value of g(x) at x = 2, and then plug this value into the function f(x).

When we don't have a specific value of x, we can simply replace the x of the outside function f(x) with the inside function g(x).

Given functions:

`f(x)=x^2+7x-10`

`g(x)=x+2`

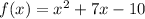
So in this case, to find (f o g)(x), we need to replace all the x's of f(x) with g(x). So as g(x) = x + 2, we replace all the x's of f(x) = x² + 7x - 10 with (x + 2):

`\begin{aligned}(f \circ g)(x)&=f(g(x))\\&=f(x+2)\\&=(x+2)^2+7(x+2)-10\\&=(x^2+4x+4)+7x+14-10\\&=x^2+4x+7x+4+14-10\\&=x^2+11x+8\end{aligned}`

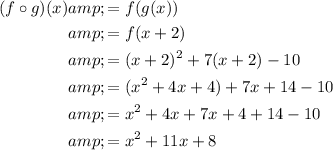
Therefore, (f o g)(x) is:

`\Large\boxed{\boxed{x^2+11x+8}}`