Question

Answer this:

Let,

`f(x) = x^2 + 7x - 10`

`g(x) = x + 2`
Solution:

`\begin{aligned}(f \circ g)(x)& = f(g(x)) \\ &=\end{aligned}`
​

Answer 1

`\sf (f \circ g)(x) = x^2 + 11x + 8`

Explanation:

Given:

`f(x) = x^2+7x-10`

`g(x) = x+2`

To find:

`(f \circ g)(x)`

Solution:

First substitute g(x) into f(x).

This means we replace x in f(x) with g(x) So, we have:

`\sf f \circ g)(x) = f(g(x)) = f(x + 2)`
Now, let's substitute x + 2 into f(x):

`\sf (f \circ g)(x) = (x + 2)^2 + 7(x + 2) - 10`
Now, expand and simplify this expression:

`\sf (f \circ g)(x) = x^2 + 4x + 4 + 7x + 14 - 10`
Combine like terms:

`\sf (f \circ g)(x) = x^2 + 11x + 18 - 10`
Simplify further, we get:

`\sf (f \circ g)(x) = x^2 + 11x +8`

Therefore,

`\sf (f \circ g)(x) = x^2 + 11x + 8`

Answer 2

`\Huge \boxed{\boxed{\bf{(f \circ g)(x) = x^2 + 11x + 8}}}`

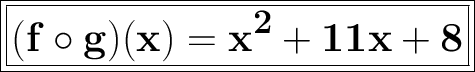
Explanation:

Given the functions
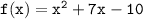`\tt{f(x) = x^2 + 7x - 10}` and
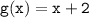`\tt{g(x) = x + 2}`, you want to find the composite function
`\tt{(f \circ g)(x) = f(g(x))}`.

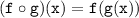To do this, substitute
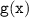`\tt{g(x)}` into
`\tt{f(x)}` wherever you see
`\tt{x}`:

• 
  `\tt{(f \circ g)(x) = f(g(x)) = (g(x))^2 + 7(g(x)) - 10}}`

Now, substitute the expression for
`\tt{g(x)}`:

• 
  `\tt{(f \circ g)(x) = (x + 2)^2 + 7(x + 2) - 10}`

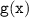Expand and simplify the expression:

• 
  `\tt{(f \circ g)(x) = (x^2 + 4x + 4) + 7x + 14 - 10 = x^2 + 11x + 8}`

So, the composite function
`\tt{(f \circ g)(x) = x^2 + 11x + 8}`.

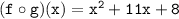#BTH1

__________________________________________________________