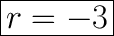Answer:
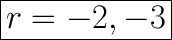
Explanation:
To solve for the values of
 where the differential equation
where the differential equation
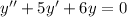 is satisfied by the function
is satisfied by the function
 , we first need to find the first and second derivatives of
, we first need to find the first and second derivatives of
 with respect to
with respect to
 , treating
, treating
 as a constant.
as a constant.
![\left[\frac{}{}y\frac{}{}\right]'=\left[\frac{}{}e^(rx)\frac{}{}\right]'](https://img.qammunity.org/2024/formulas/mathematics/high-school/1viypj6x3ffacjdj7hxxfudpbzt1vbphot.png)
↓ applying the chain rule to the right side:
![\displaystyle \left[\frac{}{}f(x)^a\frac{}{}\right]' = a \cdot f(x)^((a\, -\, 1)) \cdot f'(x)](https://img.qammunity.org/2024/formulas/mathematics/high-school/78u2xk3np9hgja3b214zoa9q57h7ykrc5d.png) where
where
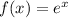 and
and

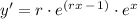
↓ simplifying using the exponent base product rule:
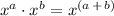
![y' = re^(\left[(rx \,-\, 1)\, +\, 1\right])](https://img.qammunity.org/2024/formulas/mathematics/high-school/latzcexw99rrw1iix9q7mx08keat04auby.png)

─────────────────────────────────
↓ taking the derivative of
 with respect to
with respect to

![y'' = \left[\frac{}{} re^(rx)\frac{}{}\right]'](https://img.qammunity.org/2024/formulas/mathematics/high-school/i0eqtl7dvb76wos1ohck7e3umy3xlre09f.png)
↓ taking out the constant (
 ) on the right side
) on the right side
![y'' = r\left[\frac{}{} e^(rx)\frac{}{}\right]'](https://img.qammunity.org/2024/formulas/mathematics/high-school/ctg550fmhcxje6se86679xmqppc58ln6a3.png)
↓ simplifying by substituting in the first derivative

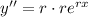

Now, we can plug these derivative expressions into the differential equation and solve for r.
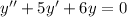
↓ plugging in the derivative expressions (think of
 as the zeroth derivative of itself)
as the zeroth derivative of itself)

↓ factoring out
 from the left side
from the left side
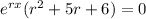
↓ factoring the second-degree polynomial factor
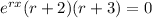
↓ splitting into 3 equations using the zero product property:

First Equation
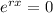
↓ taking the natural log of both sides
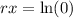
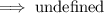
Second Equation
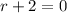
↓ subtracting 2 from both sides

Third Equation
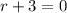
↓ subtracting 3 from both sides