Question

Consider the following functions.

f(x) = 8x², x ≥ 0; g(x)=√√8-x
Show that f and g are inverse functions algebraically.
f(g(x)) = f(
g(f(x))
=
11
= 9 ( [

Answer 1

`\begin{aligned}f(g(x))&=f\left(√(8-x)\right)\\&=x\end{aligned}`

`\begin{aligned}g(f(x))&=g\left(8-x^2\right)\\&=x\end{aligned}`

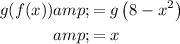
The graph of f is the reflection of the graph of g in the line y = x.

Explanation:

To show that two functions are inverses, we need to show that:

• f(g(x)) = x, for all x in the domain of g(x), and
• g(f(x)) = x, for all x in the domain of f(x).

Given functions:

`f(x)=8-x^2, \quad x\geq 0`

`g(x)=√(8-x)`

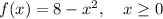
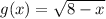
Find f(g(x)) by substituting x = g(x) into f(x):

`\begin{aligned}f(g(x))&=f\left(√(8-x)\right)\\\\&=8-\left(√(8-x)\right)^2\\\\&=8-\left(8-x\right)\\\\&=8-8+x\\\\&=x\end{aligned}`

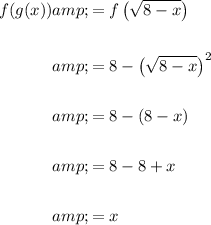
Find g(f(x)) by substituting x = f(x) into g(x):

`\begin{aligned}g(f(x))&=g\left(8-x^2\right)\\\\&=√(8-\left(8-x^2\right))\\\\&=√(8-8+x^2)\\\\&=√(x^2)\\\\&=x\end{aligned}`

Therefore, as f(g(x)) = x and g(f(x)) = x for x ≥ 0, we have successfully demonstrated that f(x) and g(x) are inverses under the given domain restriction.

If we graph the two functions (see attached), we can see that:

• The graph of f is the reflection of the graph of g in the line y = x.