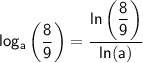Question

Rewrite the logarithm as a ratio of common logarithms and natural logarithms.

log:()
(a) common logarithms
X
(b) natural logarithms
X

Answer 1

a.)
using logarithm quotient rule
log(base a)(8/9)
=log(base a)8 - log(base a)9

Answer 2

`\textsf{Common logarithms} \sf =(log\left((8)/(9)\right))/(log(a))`

`\textsf{Natural logarithms} \sf =(ln \left((8)/(9)\right))/(ln(a))`

Explanation:

(a) Common logarithms:

The common logarithm is the logarithm with base 10.

In this case:

`\sf log_a \left((8)/(9)\right)`

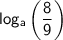
This can be expressed in terms of common logarithms (base 10) as follows:

`\sf log_a \left((8)/(9)\right)=(log\left((8)/(9)\right))/(log(a))`

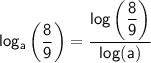
(b) Natural logarithms:

The natural logarithm is the logarithm with base e.

where e is Euler's number, approximately equal to 2.718281828459045 and commonly denoted by ln.

In this case:

`\sf log_a \left((8)/(9)\right)`

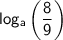
This can be expressed in terms of natural logarithms (base e) as follows:

`\sf log_a \left((8)/(9)\right)=(ln \left((8)/(9)\right))/(ln (a))`