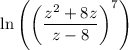Question

Use the properties of logarithms to condense the expression. (Assume z > 8.)

7[In(z) + In(z + 8)] - 7 In(z - 8)

Answer 1

`\ln \left(\left((z^2+8z)/(z-8)\right)^7\right)`

Explanation:

Given logarithmic expression:

`7\left[\ln(z)+\ln(z+8)\right]-7\ln(z-8)`

To simplify the expression, we can use the rules of logarithms.

`\boxed{\begin{array}{rl}&\underline{\sf Rules\;of\;Logarithms}\\\\\sf Product:&\ln (m)+\ln (n)=\ln(mn)\\\\\sf Quotient:&\ln (m) - \ln (n) = \ln \left((m)/(n)\right)\\\\\sf Power:&n \ln (m)=\ln(m^n)\end{array}}`

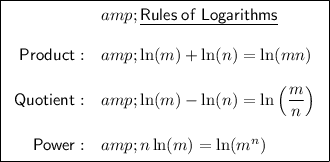
Apply the product rule to the first parentheses:

`7\left[\ln(z(z+8))\right]-7\ln(z-8)`

Simplify:

`7\ln(z(z+8))-7\ln(z-8)`

`7\ln(z^2+8z)-7\ln(z-8)`

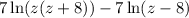
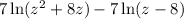
Apply the power rule:

`\ln((z^2+8z)^7)-\ln((z-8)^7)`

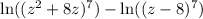
Apply the quotient rule:

`\ln \left(((z^2+8z)^7)/((z-8)^7)\right)`

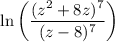
Using the power of a quotient exponent rule, this can be be written as:

`\ln \left(\left((z^2+8z)/(z-8)\right)^7\right)`