Question

Answer

nts] DETAILS LARPRECALCRMRP7 3.5.018.
ete the table for a savings account in which interest is compounded continuously. (Round your answers to four decimal places.)
Annual
Amount After
Time to
Double
% Rate
13 Years
435.21
Initial
Investment
350
ed Help?
mit Answer
Points]
Read It
DETAILS
PREVIOUS ANSWERS
LARPRECALCRMRP7 3.5.038.
e populations P (in thousands) of a certain town in North Carolina, from 2006 through 2012 can be modeled by P = 5.9ekt, where t is the year,
(a) Find the value of k for the model. Round your result to four decimal places.
k=
X
Need Help?
%
yr
(b) Use your model to predict the population in 2018. (Round your answer to the nearest person.)
people
Read It

Answer 1

Annual % rate = 1.6761% (4 d.p.)

Time to double = 41.3548 years (4 d.p.)

Explanation:

To calculate the annual interest rate of a savings account where the interest is compounded continuously, we can use the continuous compounding formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

Given values:

• Initial investment, P = $350
• Final amount, A = $435.21
• Number of years, t = 13

To find the annual interest rate (r), substitute the given values into the formula and solve for r:

`\begin{aligned}435.21&=350 \cdot e^(13r)\\\\(435.21)/(350)&= e^(13r)\\\\\ln \left((435.21)/(350)\right)&=\ln\left(e^(13r)\right)\\\\\ln \left((435.21)/(350)\right)&=13r\ln\left(e\right)\\\\\ln \left((435.21)/(350)\right)&=13r\\\\r&=(1)/(13)\ln \left((435.21)/(350)\right)\\\\r&=0.0167611937...\\\\r&=1.6761\%\;\sf(4\;d.p.)\end{aligned}`

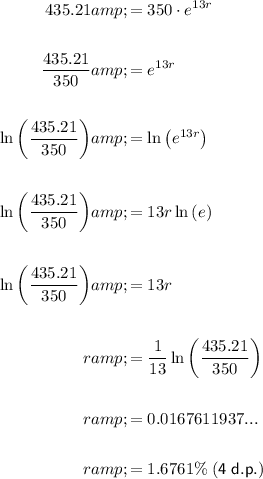
Therefore, the annual interest rate is 1.6761% (4 d.p.).

To find the time it will take for the initial investment to double, we need to find t when A = 2P.

Substitute A = 2P and the found interest rate (r = 0.016761) into the formula and solve for t:

`\begin{aligned}2P&=Pe^(0.016761t)\\\\2&=e^(0.016761t)\\\\\ln(2)&=\ln\left(e^(0.016761t)\right)\\\\\ln(2)&=0.016761t\ln\left(e\right)\\\\\ln(2)&=0.016761t\\\\t&=(\ln(2))/(0.016761)\\\\t&=41.3547628...\\\\t&=41.3548\; \sf years\end{aligned}`

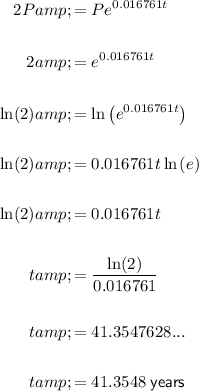
Therefore, it will take 41.3548 years for the initial investment to double.

`\hrulefill`

Note: We have used the rounded value of the interest rate in the calculation to find the number of years it takes for the initial investment to double. If we use the exact (unrounded) interest rate, the number of years is 41.3543 years (4 d.p.).